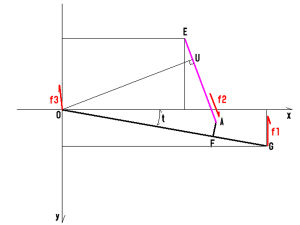
Type2(コンベンショナルタイプ)
いわゆる2本サスや、NF4などのモノサス。
各点説明
- O
- ピボット(原点)
- A
- サスペンション下部(リアフォークとサスペンションの結合部)
- E
- サスペンション上部(フレームやシートレールとサスペンションの結合部)
- F
- 点Aから線分OG(リアフォークセンター線)に下ろした垂線の足
- G
- リアアクスル
- U
- 原点から直線AEに下ろした垂線の足
つまりOUは直線AEとピボット(原点)との距離 - t
- リアフォーク(OG)とx軸のなす角
各点の添字x、yはそれぞれのx座標とy座標。
座標は直交座標でピボットを原点とし路面と水平でマシンの後方がx軸の正、路面への鉛直線方向がy軸正。
- f1
- アクスル加重
タイヤ接地点からアクスルを押し上げる力、よって鉛直成分のみ - f2
- リアサス反力
- f3
- ピボットが受ける加重
各力の添字x、yはそれぞれの力のx軸方向とy軸方向の分力。
既知の値
E(Ex,Ey):リアサス上部取り付け座標
OG:リアフォーク長(mm)
OF,AF
Gy0:リアアクスルの初期位置(mm)
k:スプリングレート(kgf/mm)
ini:プリロード(mm)
求める値
リアアクスルが j mmストロークしたときの
ratio:リンクレシオ
stroke:サスストローク
f1(f1x,f1y):アクスル加重
f2(f2x,f2y):サス反力
f3(f3x,f3y):ピボット加重
考え方
ピボット(原点O)を瞬間中心と考えると、
f1 * Gx = f2 * OU
よって
リンクレシオ:ratio = f1/f2 = OU/Gx
実際に計算する
計算内容はエクセルシートを見ながらのほうがわかりやすい(かも)
Gy = Gy0 - j
t = Asin(Gy/OG) Asin:アークサイン
Gx = OG * cos(t)
点A(Ax,Ay)を求める
∠AOF = Atan(AF/OF) Atan:アークタンジェント
OA = Sqr( AF^2 + OF^2 ) Sqr:平方根(正の値)
よって
Ax = OA * cos(t - ∠AOF)
Ay = OA * sin(t - ∠AOF)
二点A(Ax,Ay)、E(Ex,Ey)を通る直線と原点(0,0)の距離
OU = kyori_b(0,0,Ax,Ay,Ex,Ey) kyori_b:エクセルシート参照
以降 kyori_b(0,0,Ax,Ay,Ex,Ey) を kyori_b(O,A,E) という簡易表記にする
レシオを求める
上記より
ratio = OU/Gx
が計算される
この時サス長は
AE = Sqr((Ax-Ex)^2 + (Ay-Ey)^2)
となり、j=0 の時のサス長(サス自由長)を AE0 とする。
よってサスストロークは
stroke = AE0 - AE
次に加重計算
サス加重
f2 = k * (stroke + ini)
f2x = f2 * ((Ax-Ex) / AE )
f2y = f2 * ((Ay-Ey) / AE )
アクスル加重
f1 = f2 * ratio
f1x = 0
f1y = -f1
全体の釣り合いを考えると、
f1x + f2x + f3x = 0
f1y + f2y + f3y = 0
なので、
ピボット加重
f3x = -(f1x + f2x) = -f2x
f3y = -(f1y + f2y) = f1 - f2y
f3 = Sqr(f3x^2 + f3y^2)
検証
G点を瞬間中心として検証
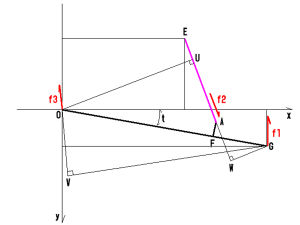
W:直線AEに点Gから下ろした垂線の足
V:f3を直線と見なし、その直線に点Gから垂線を下ろしたときの足
GW = kyori_b(G,A,E)
GV = kyori_b(G,O,f3x,f3y)
このとき
f2 * GW = f3 * GV
が成立する
F点を瞬間中心として検証
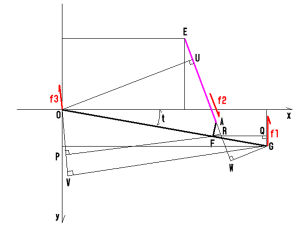
P:f3を直線と見なし、その直線に点Fから垂線を下ろしたときの足
Q:f1を直線と見なし、その直線に点Fから垂線を下ろしたときの足
R:直線AEに点Fから下ろした垂線の足
FQ = kyori_b(Fx,Fy,Gx,Gy,Gx,0) または Gx - Fx
FP = kyori_b(Fx,Fy,0,0,f3x,f3y)
FR = kyori_b(Fx,Fy,Ax,Ay,Ex,Ey)
このとき
f1 * FQ - f2 * FR = f3 * FP
が成立する
リンク比に対する検証
アクスルストロークGyが j1 mmから j2 mmに変化したとき、リアサス長が AEj1 mmから AEj2 mmに変化したとすると、ストローク量 (j1 + j2)/2 mm時のリンク比の近似値として、ratioΔ = (AEj2 - AEj1)/(j2 - j1)
が算出される。
リアサスインデックスへ